Software engineering

Convert a combination to a single number

Converting combinations into unique numbers simplifies data representation. This article explains the math behind the Fundamental Theorem of Arithmetic, prime factorization, and combinadics. Learn how these principles are applied in cryptography and data structuring.

Adnan

— 7 min read
Convert a combination to a single number

How to convert a combination to a single number and vice versa? How to count and index all combinations of elements? How to assign a unique number or rank, to any combination?

It is a math problem. Math areas like Enumerative Combinatorics or Combinatorial Number System (combinadics) have established algorithms for dealing with this and similar issues a long time ago.

This article does not dive deep into the math. It tries to provide some essential math insights to understand the problem better. The article attempts to present the problem and the solution from a more friendly perspective. Also, the time complexity of the provided source code is not in focus. Thus it is possible you will be able to find/write faster code.

Primes

Prime numbers are the building blocks of math. Other numbers are made of primes. This technique uses one of the essential math laws known as the Fundamental Theorem of arithmetic.

Fundamental Theorem of Arithmetic: any integer greater than 1 is either a prime number or can be written as a unique product of prime numbers (ignoring the order).

From another perspective: there is only one (unique!) set of prime factors for any number.

Example: 42 = 2 × 3 × 7. There is no other possible set of prime numbers that can be multiplied to make 42.

List of primes up to 1000

Knowing the Fundamental Theorem of Arithmetic, we can easily represent any combination of objects with a single number. We need to assign a unique prime number to every element. To get a unique number for any combination, multiply the assigned primes, and that’s it.

For example how to represent the combination C₁ = { "B", "D", "E" }for the setS₁ = { "A", "B", "C", "D", "E", "F", "G", "H", "I", "J", "K" }?The positions of the elements B, D, E are 1, 3, and 4. The prime numbers on the positions 1, 3, and 4 are 3, 7, and 11.
Thus, 3 × 7 × 11 = 231 represents combination C₁ = { "B", "D", "E" }

Real-life example: Cactus Kev used the Fundamental theorem of arithmetic in his Poker Hand Evaluator.

Note: The reverse process is known as prime factorization. While converting a combination to number is a swift operation, prime factorization is very slow. It is one of the reasons why it is used in cryptography.

Source: Go, JavaScript, Python.

Odometer effect

The odometer effect is what happens when a mechanical mileage counter on a car reads 9999 and then flips over to 10000. All the dials have to turn at the same time.

Car odometer

In this case, a dial represents a set. While a single dial has 10 values (0–9), a set can have any number of values, and the cardinality of each set can be different.

If we translate it to a more general form, we would say there are S₁, S₂, S₃… Sn sets and each set has N₁, N₂, N₃… Nₙ elements. How to convert a combination of n elements to a single number where each element belongs to only one set and the position of each element within a set is known?

Example, for the given sets S₁, S₂, S₃ and S₄:
S₁ = { "John", "Jack", "Joe" }
S₂ = { "Water", "Fire" }
S₃ = { "Brazil", "UK", "Russia", "Japan", "Morocco", "France" }
S₄ = { "Blue", "Red", "Yellow", "White" }
how to represent the combinations C₁ and C₂ :
C₁ = { “John”, “Fire”, “Japan”, “Red” }
C₂ = { “Joe”, “Water”, “UK”, “White” }
with the unique numbers X and Y?

Notice the odometer effect is also presented in weighted number systems (decimal, hexadecimal, octal, binary, etc.). In weighted number systems, each digit has a weight value assigned. For example, in the decimal system, the positions of digits are marked with numbers from 0 to 9, and the weight of the digit is the base (10) raised to the power of the position number.

Decimal number with the position and weight of each digit shown and derivation of the value of the number.

According to the weighted number systems, we mark every set with a position from 0 to n. Since cardinality c (the number of elements in a set) is different for each set, base-raised-to-the-power-of-position formula is not applicable anymore. The idea is the same, but the formula is slightly modified

The weight of the first set is 1, always:
w₁ = 1.

The weight of the second set is the product of the first set weight and the first set cardinality:
w₂ = w₁ × c₁ = 1 × 3 = 3.

The weight of S₃ is equal to the product of the S₂ weight and theS₂ cardinality:
w₃ = w₂ × c₂ = 3 × 2 = 6.

Similarly, for S₄:
w₄ = w₃ × c₃ = 6 × 6 = 36.

Generally: wₙ = wₙ₋₁ × cₙ₋₁

Now when we know the weight of each set, it is easy to derive the unique representation for any combination. If p is a position of an element in the set, then:

X = w₁ × p₁ + w₂ × p₂ + w₃ × p₃ + … + wₙ × pₙ;

C₁ solution

The positions of the elementsC₁ = { “John”, “Fire”, “Japan”, “Red” } are
p₁ = 0 (John)
p₂ = 1 (Fire)
p₃ = 3 (Japan)
p₄ = 1 (Red).
X = 1 × 0 + 3 × 1 + 6 × 3 + 36 × 1 = 0 + 3 + 18 + 36 = 57

57 represents John, Fire, Japan, and Red.

C₂ solution

The positions of the elementsC₂ = { “Joe”, “Water”, “UK”, “White” } are
p₁= 2 (Joe)
p₂ = 0 (Water)
p₃ = 1 (UK)
p₄ = 3 (White).
Y = 1 × 2 + 3 × 0 + 6 × 1 + 36 × 3 = 116

116 represents Joe, Water, UK, and White.

Source code: Go, JavaScript, Python.

Combinadics

What if there is a single set of N elements and we need to represent a combination of x elements (a real-life example is a lottery)? It is a classic combinadics problem.

Since this example requires more than essential math skills, more than knowledge of multiplying and adding numbers, the article is not going into the details.

For example, how to represent the combination C₁ = { "C", "G", "K" } for the given set: S₁ = { "A", "B", "C", "D", "E", "F", "G", "H", "I", "J", "K" }?

The indices for the elements C, G, K are 2, 6, 10 respectively (reversed c₁ = 10, c₂ = 6 and c₃ = 2).

According to the combinadics, the bijection is the following:

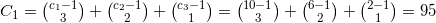
Bijection for the previous example

As already noted, the article is not going to step deep into the math. If you are not familiar with combinatorics or you do not know how to work with the binomial coefficient, you can copy the binomial code from here.

More on this topic can be found here and here.

Source code: Go, JavaScript, Python.

Bit Flags

This technique is well known and widely used. The idea behind the bit flags is not to convert a combination to a single number but to hold multiple values into a single variable. The bit flags technique is convenient for sets of few elements only; usually, it is used with enumerated values.

The smallest unit of memory is a bit. The smallest addressable unit is a byte (a group of 8 bits). It means that every variable must be at least 1 byte in size. One byte can hold ²⁸=256 unique values. For most data types, it is okay. However, boolean types (boolean type has only two values: true or false) need only 1 bit to store the value. Thus, 1 byte can hold up to 8 boolean values.

For example how to represent the combination C₁ = { "C", "F", "H" } for the set S₁ = { "A", "B", "C", "D", "E", "F", "G", "H", "I", "J", "K" }?

The indices for the elements C, F, H, are 2, 5, 7, respectively. If we use bit flags to store the positions of combination elements, we get: 10100100 (put 1 on positions 2, 5, and 7, starting from right to left).

(10100100)₂ equals to (164)₁₀.

The answer to the previous question is 164.

If bit flags are still not clear to you, I advise you to analyze IPv4 addresses and IPv4 address subnetting — it is based on bit manipulation.

Source code: Go, JavaScript, Python.

Final word

A separate article (or a book) could be written on any of the presented techniques. In most cases, the position of an element within the set is essential (the value of the element is less important).

There are many other ways to derive a single number from the combination. As a professional, I have used only these four, and that is the main reason why I choose to write about them. Way back when I was a rookie, I struggled to figure out how to convert a combination to a single number, and without the right background, it was hard even to google it. Hopefully, this article is a good clue on a path of converting combinations to a number.

Related Readings

As an addition, a few connected readings:

Read more